Ice Growth: Thin to Thick
Summary:
There are a couple of pretty good methods for predicting ice growth. One was developed by George Ashton in 1989 and is based on freezing degree days. It is a good, general purpose method when you do not have a good feel for the conditions other than temperature. The second method is the Swedish method has been developed by Martin Ajne (and others?). It uses a combination of air temperature, wind speed and radiational cooling. It is most accurate for thin ice (up to a couple inches). It is handy for guessing how much ice will form over night or in the next day or two. It is described near the end of this page.
The Ashton Ice Growth Prediction Method
Once the first layer of ice catches on a lake it grows thicker at rate that is dependent on air temperature, windiness, radiational cooling, the thickness of the ice sheet and any snow or frost buildup on the ice sheet. Temperature is the easiest to assess. Freezing degree days (FDD) are the average number of degrees below freezing over 24 hours. For example is the average temperature over a day is 17 degrees that day had fifteen FDDs. An ice sheet will, in theory, grow at a rate of roughly one inch per fifteen FDDs starting from ice between 1/2" and 3" thick (as the ice gets thicker the growth rate decreases as a result of the thermal resistance of the thicker ice). This is based on there being a bit of wind, a reasonably clear sky and no snow/frost on the ice. If there is no wind or there are cloudy skies, the ice growth may be considerably slower.
For example, starting from 2" ice, if the maximum temperature yesterday was 22 degrees and the minimum overnight was 12 degrees the average is 17 deg giving 15 FDDs for the 24 hour period. This method assumes a typical amount of cloudiness and day-night temperature profile. The ice should be about an inch thicker than yesterday. As explained below there are a number of reasons why 'your results might vary'. Even a thin layer of snow or thick frost will dramatically slow the growth rate. As always, check the ice itself to see what the ground truth is.
27 mm(1.06") ice: Not quite enough to stay on top. It needs another 1 mm to barely support 175 lb. To have a reasonable safety factor it needs another 20 or 30 freezing-degree-days to make it thick enough.
For an ice sheet to grow thicker it has to dissipate 80 calories per gram of water that turns to ice. The heat has to get out of the ice sheet either by conduction and convection into overlying air or by radiational cooling from the ice surface. In general, when the ice is thinner than 3" the cooling rate is limited by the ability of the air over the ice to transmit heat. Thin ice at temperatures near freezing thickens most quickly when radiaional cooling conditions are best (clear sky, low humidity).
Note: Ice thickness is not the only thing that matters with bearing strength. With cold (fully frozen) ice, thickness pretty much tells the story with strength. Thawed ice can be anywhere from a little weaker to much weaker than cold ice.
Catching:
Before the ice can get thick it has to 'catch', forming the primary ice layer that grows into something we can skate, fish, sail and drive on. There several conditions that support ice catching:
The bulk water water needs to be cool enough (typically in the 35-37 degree range). Cooling of the bulk water correlates with the water depth. Winds in the low single numbers for a few hours is often what allows a new ice sheet to form and survive. See: Ice physics for recreational ice-users for more on this and many other aspects of ice growth.
Once the bulk temperature gets to 39 degrees or colder (maximum density) it is convectivley stable if there is no wind to mix the water. The water surface cools from radiational cooling, cold air with light wind. The lake is most likely to form ice when winds are light which is also when the air temperature is colder and skies are clear. In this circumstance radiational cooling accounts for most of the ice growth. A clear sky allows radiation to remove energy from the surface at a rate of about 70 watts/square meter. This helps establish a thin, supercooled layer that typically starts to form ice at about half a degree (F) of supercooling.
For the first crystals to form on the supercooled surface layer something needs to nucleate them. Ice is the best nucleating agent for this. Examples include snow, and ice fog. Lake water is also full of fine sediment, bacteria and other things that can act as nucleating agents. If it is moderately cold, calm and with no snow falling, large crystals form (few nucleation sites). This is called unseeded ice. The nucleation sites are most likely particulates in the water. If snow is falling small ice crystals form on the water surface (lots of nucleation sites). This is called seeded ice and the crystal size of the primary and secontary ice is small (under 1/2" typical).
The following graphs are based on a formula proposed George Ashton in 1989. It covers both thin and thick ice. The 100+ year old Stephan solution works well with an adjustment coefficient of 0.5 to 0.8 for thicker ice or very cold conditions but dramatically overestimates the growth rate of thin ice and less severe temperatures. The Stephan solution does not factor in the heat transfer capacity of the air over the ice sheet but the Ashton formula does. Neither directly factors in radiational cooling, solar heating, wind, snowcover and other factors that can affect ice growth rates however by using adjustment coefficients they approximate the effect of some of these factors. The following charts show calculated growth rates for different periods of time. This can be handy for making a rough guess of growth over time at a constant temperature. As always, actual measurements of thickness trump calculated numbers.
Reality is more complicated. The temperature is rarely constant for more than a few hours. Radiational cooling on a clear night can be the major part of the cooling effect (thin ice grows at above freezing temperatures in this situation). Sun angle is a big factor as is the presence or lack of sun, especially later in the season. Cold wind increases heat removal from the top of the ice. Snow is a very effective insulator and it dramatically slows growth. Slush on the surface or as a layer within the ice sheet (layered ice) stops growth on the bottom of the ice sheet until the slush layer is fully frozen.
These graphs are of most practical use to determine how much an ice sheet is likely to grow in a day or two of fairly constant temperatures. For example if you have bare ice that 2" thick and it is going to average 10 degrees for the next two full days, the ice will probably grow to about 5" in that time. As with everything else about ice, make sure you measure what the ground truth is (and don't use your truck as your testing tool). There are lots of reasons it could have grown less than expected and not many that it might have allowed it to grow more.
Related to this, the temperature data for several of the 2013 season fatalities shows they were preceded by several days of temperatures that held near freezing. Many important details about the incidents are not known but it does appear likely that ice in these circumstances may slowly thaw. Thawing is, on average, about 30% faster than growth which is probably part of this story.
The following graph from Ashton's paper Thin Ice Growth shows reality against the calculated estimate. The upper three lines are the Stephan Solution with adjustment factors of 0.5, 0.7 and 1.0. The lower three lines are for the Ashton approach with the lines representing different values of the bulk heat transfer coefficient from ice top surface to air well above the ice (Hia). I used a value of Hia of 20 in making the graphs shown above as that best represents the empirical data. This is based on conditions similar to the St Lawrence River. If the area you are interested in is less windy, expect slower ice growth. (December-January winds on the St Lawrence River average about 9 mph with average gusts at 22).
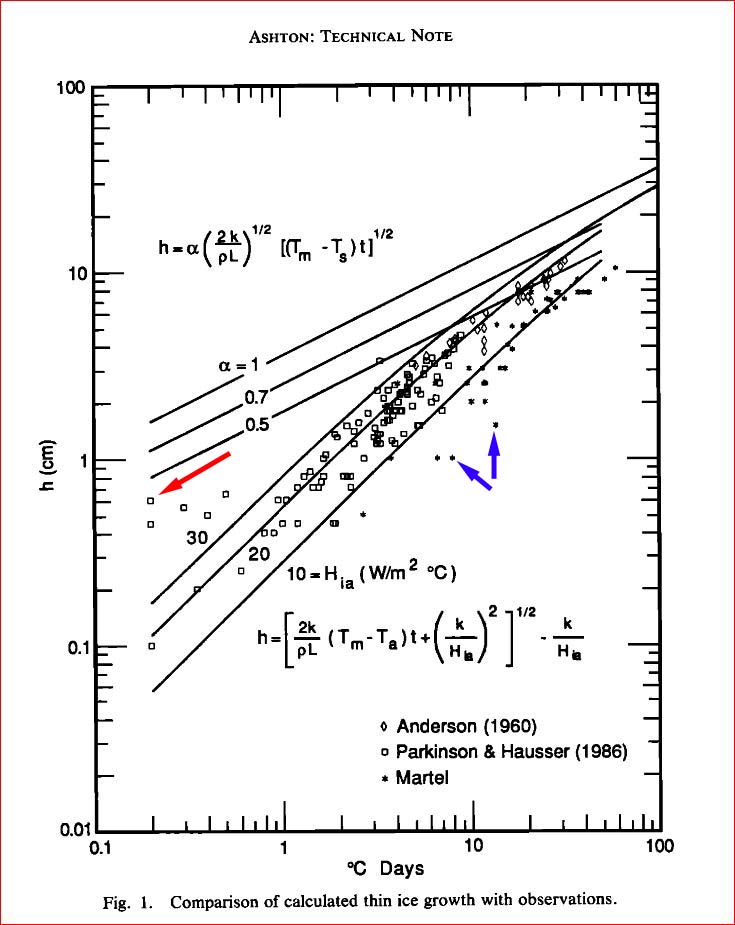
Most of the data falls within a factor of 2 the predicted value at Hia=20. The extreme cases at low thicknesses (1/4" thick, red arrow) that freeze faster than the average by nearly 10 times. This may well be a situation where the temperature is slightly below freezing and radiaitional cooling is the main cooling mechanism. The blue arrows point to growth rates that are slower than typical. Sunny weather , calm winds, cloudy skies or snow are possible contributors to this.
The Swedish Ice Growth Prediction Method:
For a more nuanced look at growth of thin ice (less than a couple of inches) have a look at Marten Ajne's book Ice Physics for Recreational Ice-Users. It gives the following rules of thumb for thin ice growth in snow free conditions:
The sum of:
- 0.05mm/h for every negative degree (C) of air temperature
- 0.02 mm/hr for times the product of wind speed (m/s) and negative air temperature
- 0.7 mm/hr for 100% clear skies and nothing for completely clouded.
For example if the temperature is 32 degrees F, there is no wind and the sky is clear about 1/3 of an inch will form overnight (12 hours) as a result of radiational cooling alone. If the sky is cloudy and calm the temperature will have to be about 7 degrees (F) to grow 1/3" of ice in 12 hours. If it is cloudy and there is a 10 mph wind the temperature will have to be 27 degrees F to grow 1/3" of ice in 12 hours. This assumes there is a layer of ice on the water that is thick enough to fend off the 10 mph wind. If you have clear skys, cold temperatures (15 deg F) and wind (15 mph) this method predicts about 1.8" of ice will grow in 12 hours.
Both the Ashton and Ajne approaches are easiest to use if you put the algorithms in a spreadsheet. Click here for a spreadsheet set up for the Ajne approach (in .ods format-OpenOffice).
Click here for an Excel ( .xls) version
More Information
For a more substantial discussion of this and other dynamic processes on ice I highly recommend a copy of Ice physics for recreational ice-users by Mårten Ajne. If you have read this far in this article you should have a copy of his book.
Click Here for a bit more insight into the role of different factors on thin ice growth from Marten Ajne.
Click here to see George Ashton's paper: Thin Ice Growth. It was published in WATER RESOURCES RESEARCH,VOL. 25, No 3, Pages 564-566, March 1989.
For a look at Jan-Erik Gustafsson's forecast method skating ice, see the January 24, 2012 Blog entry or go directly to his North American Forecast Site.
Reference to a paper on radar ice thickness in Canada
Click here for more info on bearing strength.
Bob
